B树也称B-树,它是一颗多路平衡查找树。B树的定义：

  1. 每个节点最多有m-1个关键字（可以存有的键值对）
  2. 根节点最少可以只有1个关键字
  3. 非根节点至少有m/2个关键字
  4. 每个节点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
  5. 所有叶子节点都位于同一层，或者说根节点到每个叶子节点的长度都相同
  6. 每个节点都存有索引和数据，也就是对应的key和value。

描述一颗B树时需要指定它的阶数，阶数表示了一个节点最多有多少个孩子节点，一般用字母m表示阶数。根节点的关键字数量范围：1 <= k <= m-1，非根节点的关键字数量范围：m/2 <= k <= m-1。比如这里有一个5阶的B树，根节点数量范围：1 <= k <= 4，非根节点数量范围：2 <= k <= 4。

插入

插入18，70，50，40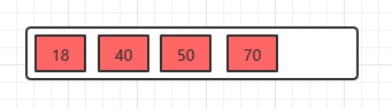
image.png
插入22，发现这个节点的关键字已经大于4了，所以需要进行分裂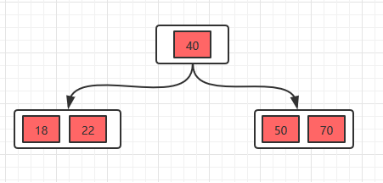
image.png
接着插入23，25，39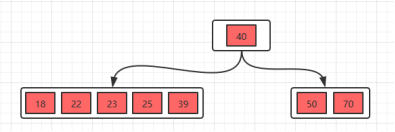
image.png
分裂

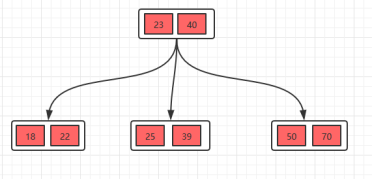
image.png

删除

初始状态是下面这样的B树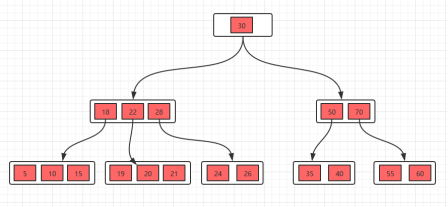
image.png

  1. 删除15，这种情况是删除叶子节点的元素，如果删除之后，节点数还是大于m/2，这种情况只要直接删除即可

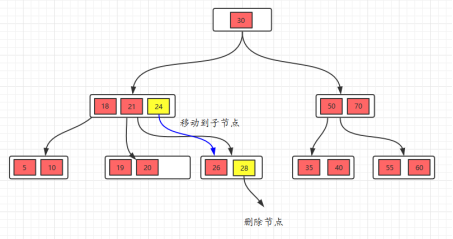
image.png

  1. 删除22，这种情况的规则：22是非叶子节点，对于非叶子节点的删除，我们需要用后继key（元素）覆盖要删除的key，然后在后继key所在的子支中删除该后继key。所以将后继元素24移到被删除的22所在的节点。

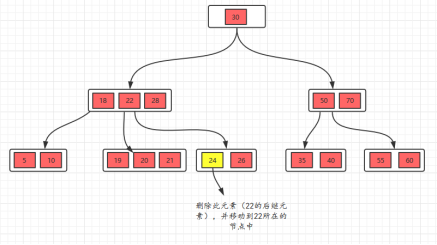
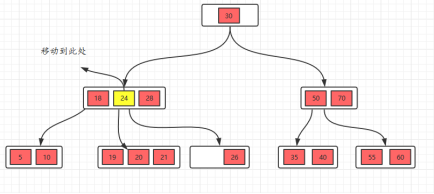
image.pngimage.png
此时发现26所在的节点只有一个元素，小于2个（m/2），这个节点不符合要求，这时候的规则（向兄弟节点借元素）：如果删除叶子节点，如果删除元素后元素个数少于（m/2），并且它的兄弟节点的元素大于（m/2），也就是说兄弟节点的元素比最少值m/2还多，将先将父节点的元素移到该节点，然后将兄弟节点的最后一个元素再移动到父节点。（右旋）
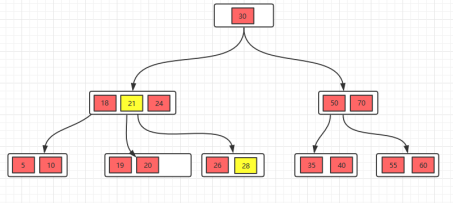
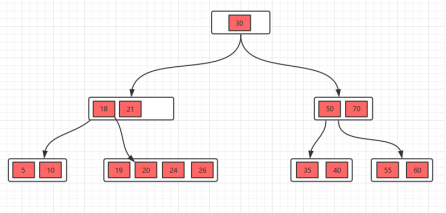
image.pngimage.png

  1. 接着删除28，删除叶子节点，删除后不满足要求，所以，我们需要考虑向兄弟节点借元素，但是，兄弟节点也没有多的节点（2个），借不了。如果遇到这种情况，首先，还是将先将父节点的元素移到该节点，然后，将当前节点及它的兄弟节点中的key合并，形成一个新的节点。

image.pngimage.png