每一个节点最多含有两个子树的树称为二叉树。在二叉树的概念下又衍生出满二叉树和完全二叉树的概念。
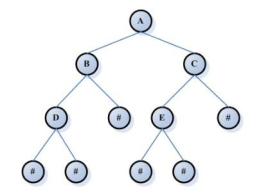
满二叉树
除最后一层无任何子节点外,每一层上的全部结点都有两个子结点。也能够这样理解,除叶子结点外的全部结点均有两个子结点。节点数达到最大值,全部叶子结点必须在同一层上
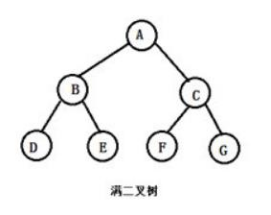
完全二叉树
若设二叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最大个数,第h层全部的结点都连续集中在最左边,这就是完全二叉树。
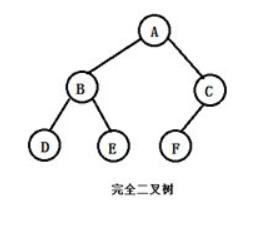
二叉树的遍历方式:遍历顺序
- 先序遍历:先根节点->遍历左子树->遍历右子树
- 中序遍历:遍历左子树->根节点->遍历右子树
- 后序遍历:遍历左子树->遍历右子树->根节点
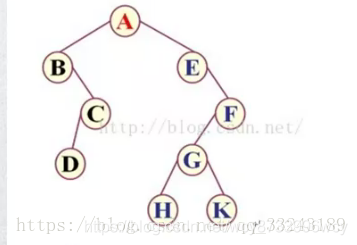
示例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
| package test;
import lombok.Data;
@Data
public class TreeNode {
private String value;
private TreeNode left;
private TreeNode right;
public TreeNode(String value) {
this.value = value;
}
@Override
public String toString() {
return "TreeNode{" +
"value='" + value + '\'' +
'}';
}
public void preOrder() {
System.out.print(this.getValue());
TreeNode leftChild = this.getLeft();
if (leftChild != null) {
leftChild.preOrder();
}
TreeNode rightChild = this.getRight();
if (rightChild != null) {
rightChild.preOrder();
}
}
public void infixOrder() {
TreeNode leftChild = this.getLeft();
if (leftChild != null) {
leftChild.infixOrder();
}
System.out.print(this.getValue());
TreeNode rightChild = this.getRight();
if (rightChild != null) {
rightChild.infixOrder();
}
}
public void postOrder() {
TreeNode leftChild = this.getLeft();
if (leftChild != null) {
leftChild.postOrder();
}
TreeNode rightChild = this.getRight();
if (rightChild != null) {
rightChild.postOrder();
}
System.out.print(this.getValue());
}
}
package test;
import cn.hutool.core.util.ObjectUtil;
import lombok.Data;
@Data
public class BinaryTree {
private TreeNode root;
public void setRoot(TreeNode root) {
this.root = root;
}
public void preOrder() {
if (ObjectUtil.isNotEmpty(root)) {
root.preOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
public void infixOrder() {
if (ObjectUtil.isNotEmpty(root)) {
root.infixOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
public void postOrder() {
if (ObjectUtil.isNotEmpty(root)) {
root.postOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
}
package test;
public class Test {
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
TreeNode A = new TreeNode("A");
TreeNode B = new TreeNode("B");
TreeNode C = new TreeNode("C");
TreeNode D = new TreeNode("D");
TreeNode E = new TreeNode("E");
TreeNode F = new TreeNode("F");
TreeNode G = new TreeNode("G");
TreeNode H = new TreeNode("H");
TreeNode K = new TreeNode("K");
A.setLeft(B);
B.setRight(C);
C.setLeft(D);
A.setRight(E);
E.setRight(F);
F.setLeft(G);
G.setLeft(H);
G.setRight(K);
tree.setRoot(A);
System.out.print("前序遍历测试 ");
tree.preOrder();
System.out.println();
System.out.print("中序遍历测试 ");
tree.infixOrder();
System.out.println();
System.out.print("后序遍历测试 ");
tree.postOrder();
}
}
执行结果:
前序遍历测试 ABCDEFGHK
中序遍历测试 BDCAEHGKF
后序遍历测试 DCBHKGFEA
|
二叉查找树:有顺序的树
二叉查找树定义:又称为是二叉排序树(Binary Sort Tree)或二叉搜索树。二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 左、右子树也分别为二叉排序树;
- 没有键值相等的节点
二叉查找树相比于其余数据结构的优点在于查找、插入的时间复杂度较低为O ( log n ) 。二叉查找树进行中序遍历,即可得到有序的数列,二叉查找树的高度决定了二叉查找树的查找效率。
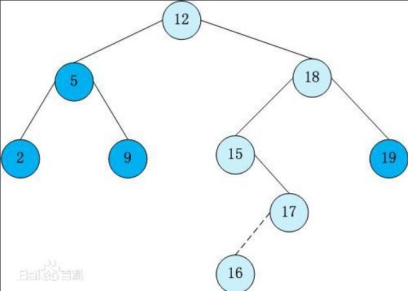
二叉查找树也会存在某些特殊情况,因此我们就需要平衡二叉树来提高二叉查找树的查找效率

平衡二叉树AVL
一棵AVL树是其每个结点的左子树和右子树的高度最多相差1的二叉查找树(空树的高度为-1),这个差值也称为平衡因子(其取值可以是1,0,-1,平衡因子是某个结点左右子树层数的差值。
为什么要让高度差不超过1?这样才能保证整棵树的深度最小。我们可以看到,其高度一般都良好地维持在O(log(n)),大大降低了操作的时间复杂度。
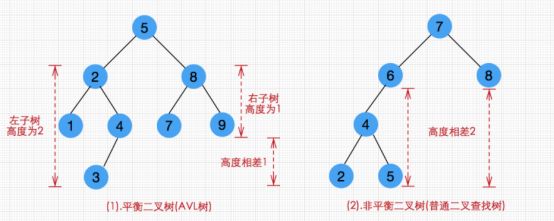
引起结点数量变化的操作才可能导致平衡被改变,也就是删除和插入操作

可以通过对树进行简单的修复来让其重新恢复到平衡,而这样的简单操作我们就称之为旋转,当然旋转也有单旋转和双旋转之分。
假设结点X是失衡点,它必须重新恢复平衡,由于任意结点的孩子结点最多有两个,而且导致失衡的必要条件是X结点的两棵子树高度差为2(大于1),因此一般只有以下4种情况可能导致X点失去平衡:
- 在结点X的左孩子结点的左子树中插入元素
- 在结点X的左孩子结点的右子树中插入元素
- 在结点X的右孩子结点的左子树中插入元素
- 在结点X的右孩子结点的右子树中插入元素
第一情况和第四情况是对称的,可以通过单旋转来解决,而第二种情况和第三情况是对称的,需要双旋转来解决。
左左单旋转(LL)
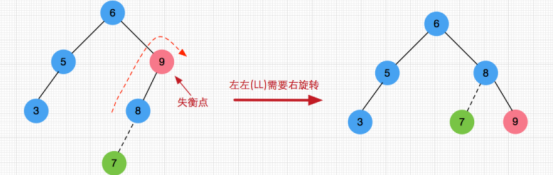
左图在原始AVL树插入7结点后,结点9变为失衡点,树再满足AVL性质,因此需要对9结点进行左左单旋转(即向右旋转)后,得到右图。此时不需要操作树的根结点(6)。
右右单旋转(RR)
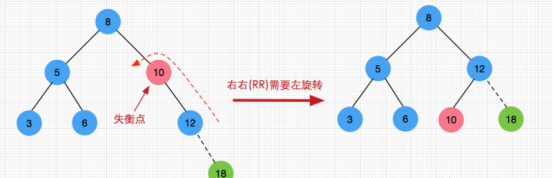
左右双旋转(LR)
- 第一次旋转:图1这里我们可把5、6组成的子树看成前面的右右旋转情景,进行左向旋转,得到图2。5变为6的左子树同时6的左子树,7变成6的右子树,其他不变,到此第一次旋转完成。
- 第二次旋转:将6、8组成的子树看作左左情景,进行向右旋转,由图2得到图3。8变成6的右孩子结点,并且6的右子树7变成8的左子树,第二次旋转完成。树也重新恢复到平衡。
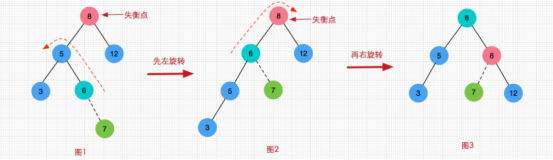
右左双旋转(RL)
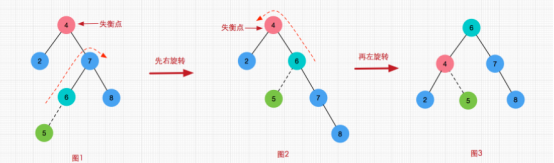
如何判断进行单旋转还是双旋转
- 单旋转: 插入点不介于 不满足AVL条件的树根 和 树根对应孩子节点之间
- 双旋转:插入点介于不满足AVL条件的树根 和 树根对应孩子节点之间












